Лаборатория ЛККМ

фото Луцик В.И.

Заведующий сектором

Луцык Василий Иванович

доктор химических наук, профессор
Email: vluts@ipms.bscnet.ru
Тел.: +7(3012)41-58-63

Состав подразделения:

Общая численность 7 человек, в том числе
– 2 доктора наук,
– 2 кандидата наук,
– 2 аспиранта.

Список штатных сотрудников

Луцык Василий Иванович, – зав. сектором, д.х.н., проф., vluts@ipms.bscnet.ru
Воробьева Вера Павловна, – в.н.с., д.ф.-м.н., доц., vvorobjeva@mail.ru
Зеленая Анна Эдуардовна, – с.н.с., к.ф.-м.н., zel_ann@mail.ru
Насрулин Эдуард Рафаэльевич, – н.с., nased@bk.ru
Зырянов Александр Михайлович, – н.с., zam1979@list.ru
Ламуева Марина Владимировна, – м.н.с., marina_bgu@mail.ru
Балданов Виктор Дашиевич, – асп, victor_baldanov@mail.ru
Парфенова Мария Дмитриевна, – асп, krygentul@gmail.com

Важнейшие научные результаты

Важнейшие публикации

Патенты, изобретения

Официальное признание

Связь с вузами

Краткая историческая справка о подразделении:

Сотрудники сектора компьютерного конструирования материалов переведены в состав Отдела физических проблем, преобразованного позже в Институт физического материаловедения, из Бурятского института естественных наук СО РАН. Научное направление сектора сформулировано в диссертации В.И.Луцыка «Гетерогенный дизайн: компьютерное конструирование многокомпонентных систем по уравнениям границ гомогенных областей» (д.х.н., 1997). Дальнейшее развитие этого направления связано с выполнением проектов РФФИ 98-03-32844 «Дизайн микроструктур многокомпонентных материалов по уравнениям границ однофазных областей» (1998-2000), 01-03-32906 (и одноименный молодежный проект Б.В.Мохосоева) «Генотип гетерогенного материала (границы концентрационных доменов с уникальными схемами фазовых превращений и термодинамически неустойчивых фрагментов фазовых областей в многомерных диаграммах известных и прогнозируемых топологических типов)» (2001-2003), 05-08-17997 «Компьютерные рабочие модели T-x-y диаграмм для конструирования гетерогенных материалов» (2005-2008), Лаврентьевского молодежного проекта СО РАН № 68 «Машинная графика фазовых диаграмм четверных систем» (2006-2007) и с защитами диссертаций А.Э.Зеленой «Повышение информативности математических моделей изобарных фазовых диаграмм визуализацией на проекциях пентатопа и расчетом конод» (к.ф.-м.н., 2002), О.Г.Сумкиной «T-x-y-z диаграмма с двойным инконгруэнтным соединением: геометрическое строение, схемы кристаллизации, баланс масс» (к.ф.-м.н., 2002), В.П.Воробьевой «Фазовые диаграммы состояния трех- и четырехкомпонентных систем: от топологии к компьютерным моделям» (д.ф.-м.н., 2012).

Гетерогенный дизайн является инновацией физико-химического материаловедения (раздел технической физики), исследующего закономерности и механизмы образования фаз в равновесных и неравновесных условиях. Так как экспериментальные исследования и термодинамический расчет не являются достаточными условиями для того, чтобы многокомпонентные фазовые диаграммы состояния (далее – ФД) становились реальным рабочим инструментом материаловеда и позволяли ему открывать закодированные в них сведения о результатах взаимодействия исходных компонентов, то необходима сборка многомерной ФД из соответствующих (гипер)поверхностей или фазовых областей. Причем, первый вариант сборки ФД затрудняет использование ее для анализа материальных балансов, тогда как при монтаже ФД из фазовых областей появляется больше возможностей, вплоть до расшифровки генотипа гетерогенного материала.

Области исследования:

Фторид-хлоридные системы для расплавлено-солевого реактора 4-го поколения
Оксидные и халькогенидные системы для получения функциональной керамики и термоэлектрических материалов
Силикатные системы для совершенствования технология получения строительных материалов
Fe-Ni-R-S (R=Cu, Co) системы для оптимизации пирометаллургических технологий извлечения никеля, меди, кобальта
Системы с расслаиванием расплава для синтеза тугоплавких боридов, силицидов и интерметаллидов
Боратные системы для выращивания монокристаллов
Металлические системы со сменой типа трехфазной реакции для разработки титановых и циркониевых сплавов
Металлические системы для бессвинцовых припоев

Важнейшие научные результаты:

1. Отработан алгоритм сборки пространственной модели ФД: пространственная схема моно- и нонвариантных реакций, расширяющая возможности традиционной таблицы Шейла; согласование экспериментальных данных и термодинамических расчетов для замыкания контуров нелинейчатых поверхностей; содержательное обозначение всех геометрических элементов.

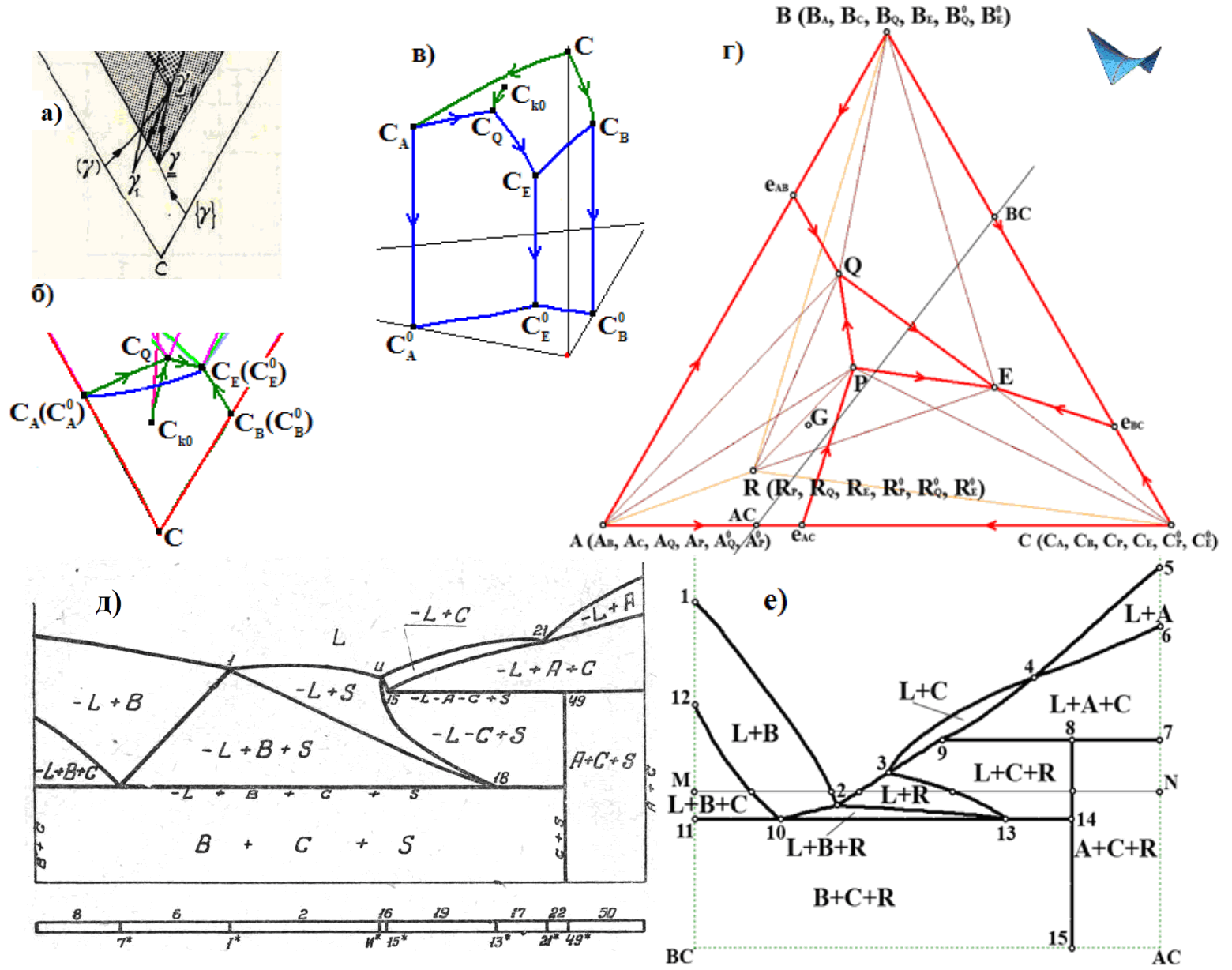
Рис. 1. В [A.Prince. Alloy Phase Equilibria. 1966] сольвус C_AC_QC_EC⁰_EC⁰_A с ортогональными C_AC⁰_A, C_EC⁰_E (а-в) должен замыкаться (С_k0C_Q – квазискладка солидуса).

В [Л.С.Палатник, А.И.Ландау. Фазовые равновесия в многокомпонентных системах. 1961] граница областей L+C и L+C+S(R) должна опускаться (г-е) от плоскости реакции L+A+C→S(R)

2. При поиске эффективных технологий сборки ФД апробированы: 1) методы аппроксимации (гипер)поверхностей Т-х-у и Т-х-у-z диаграмм - а) по заданному аддитивному контуру, б) перемещением образующих элементов (кинематический метод), в) минимизацией площади при произвольном контуре; 2) идеологии создания программных продуктов – а) уникальная модель ФД, б) редуцируемая модель ФД, в) редакторы и конструкторы ФД; 3) принципы сборки ФД – а) из (гипер)поверхностей, б) из фазовых областей.

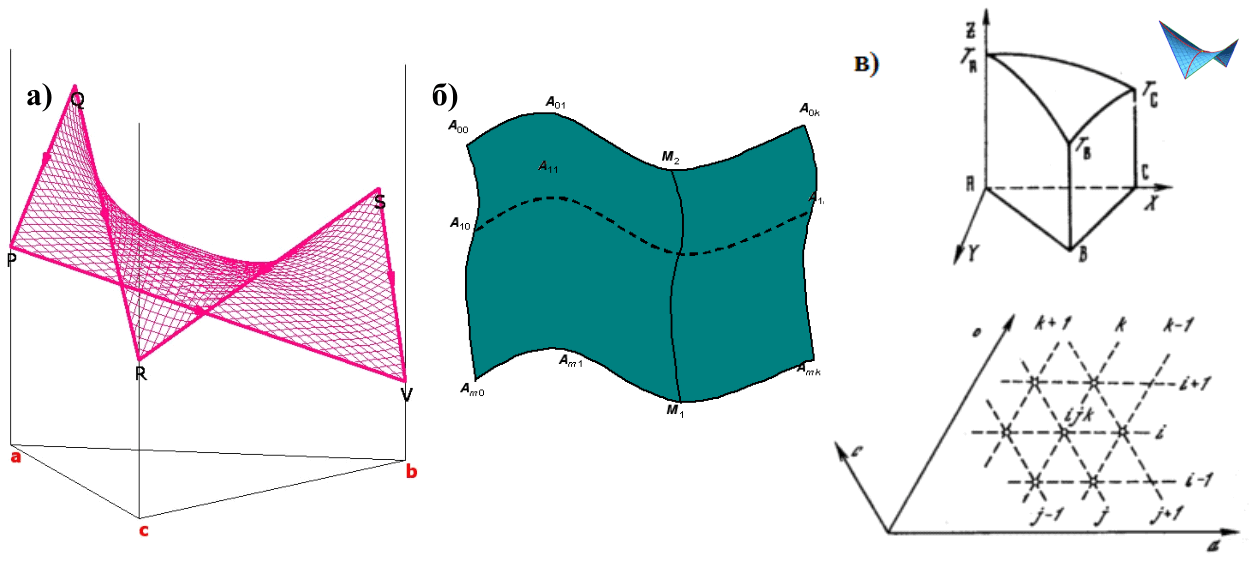
Рис. 2. Аппроксимация поверхностей: аддитивный контур (а), перемещение образующей М₁М₂ по направляющим А₀₀А₀₁…A_0k, А₁₀А₁₁…A_1k, …, А_m0А_m1…A_mk (б), минимальная площадь при произвольном контуре (в)

3. Разработана технология визуализации вертикальных (для заданного состава) и горизонтальных (изотерма изоплеты) материальных балансов, позволившая, в частности, учесть конкуренцию разнодисперсных кристаллов (рис. 3) и выявить новые характеристики трехфазной области со сменой типа реакции (рис. 4).

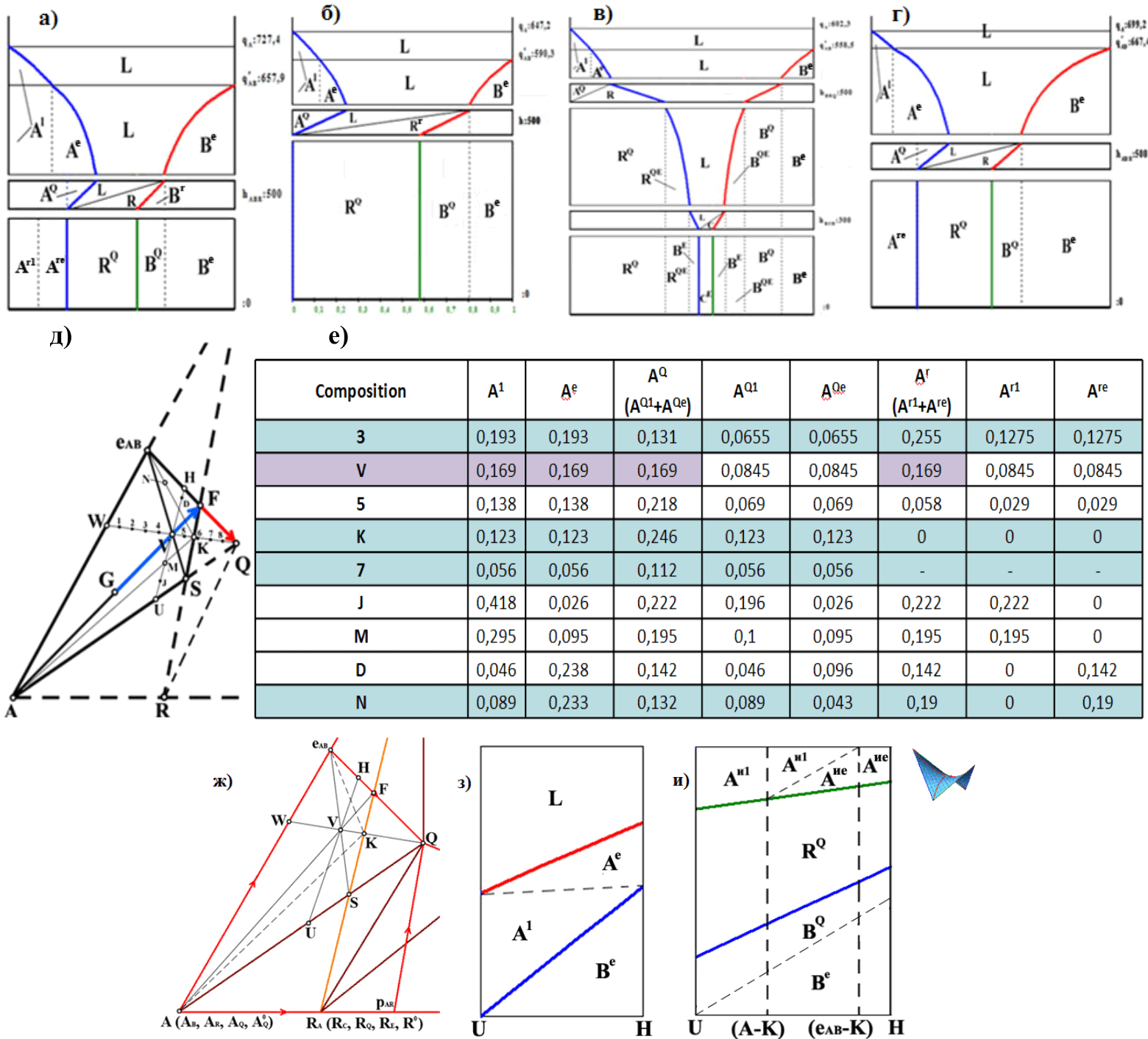
Рис. 3. Поле Ae_ABFS в ФД с инконгруэнтным соединением R=A₃C (д,ж) состоит из фрагментов е_ABFК, Ае_ABК, АSК с микроструктурами М+А^е, М+А^е+А¹, М+А¹, где М=R^Q+В^Q+В^е. (а-г) – Матбалансы составов 3, K, 7, N. (з,и) - Матбалансы изоплеты UH при T_Q+δ и T_Q-δ. Выявлены «замечательные» линии АF (А^е=А^Q); е_ABS (А¹=А^Q); WQ (А¹=А^е) и точка V (А¹=А^е=А^Q=А^r), где r - остаток после реакции L+А_Q=В_Q+R_Q). В отличие от трехмерного поля QFS, двухмерное поле QF отличается отсутствием реакции L¹→A¹, Однако, вследствие конкуренции кристаллов A¹ и A^e, оба поля обладают одной и той же микроструктурой, т.е. QF∈QFS и не является уникальным.

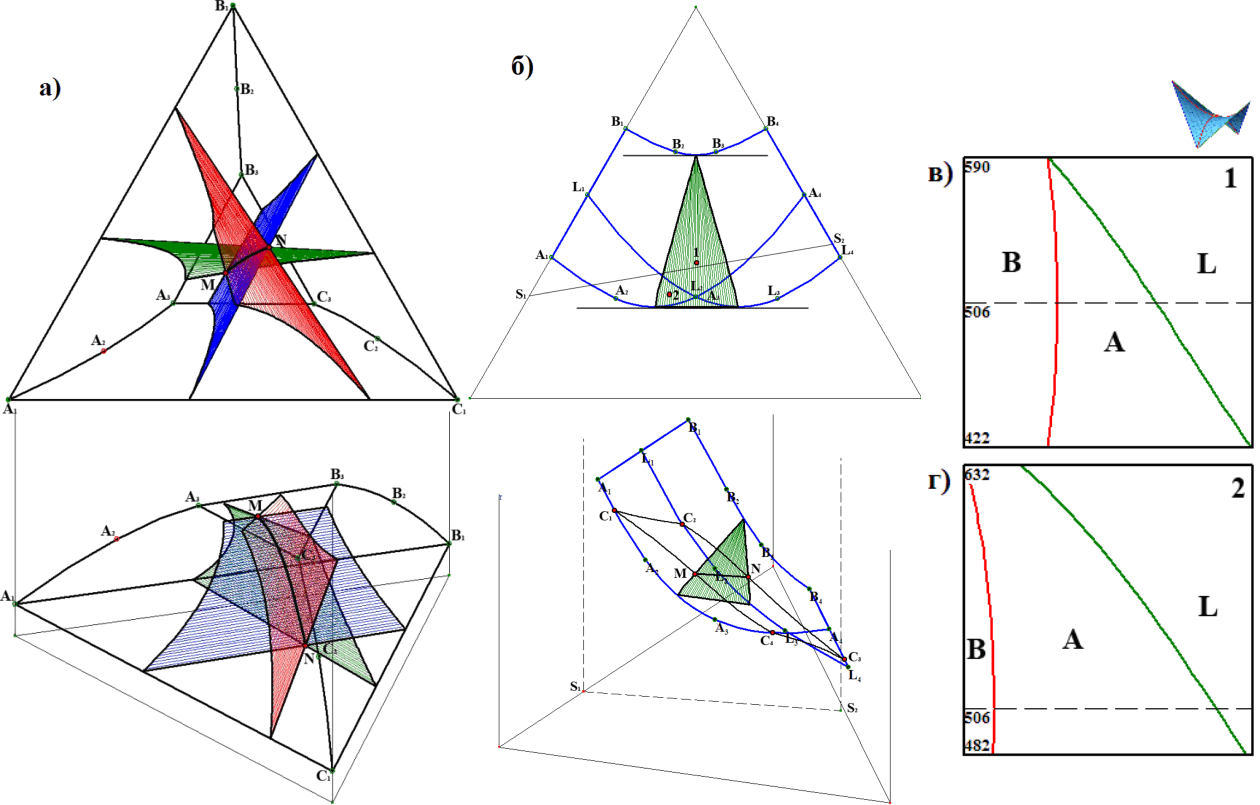
Рис. 4. Поверхности двухфазных реакций в области A+B+C (при смене знака приращения массы третьей фазы в процессе охлаждения гетерогенного материала) – (а). Подтверждение матбалансами изотермичности трехфазной трансформации по А.В.Cторонкину [ЖФХ. 1971. Т. 45, № 5. С. 1210-1213] – (б-г).

4. При дизайне сплавов учитывается разбиение трехфазных областей на фрагменты с различной динамикой приращения масс.

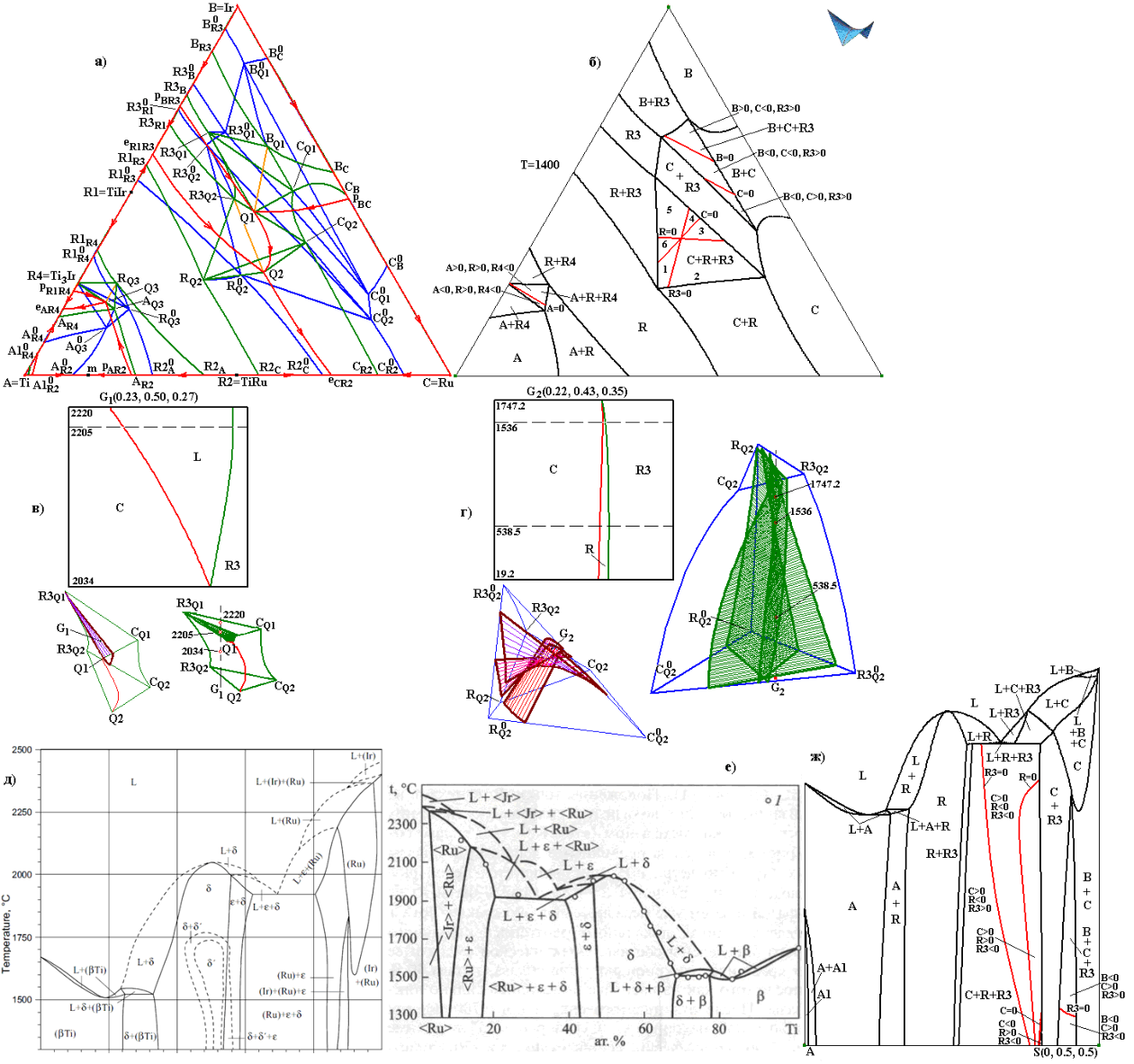
Рис. 5. Проекция ФД Ti-Ir-Ru (а) и ее изо- (б) и политермический (ж) - Ti-S(0, 0.5, 0.5) - разрезы с разбиением трехфазных областей на фрагменты, и с подтверждением (ж) потери (д) [MSIT, G.Effenberg, S.Ilyenko. SpringerMaterials - The Landolt-Börnstein Database (http://www.springermaterials.com/docs/info/10916070_53.html] области L+ε [Еременко В.Н. Избранные труды. Воспоминания. 2011]. (в,г) - Матбалансы в областях L+C+R3 и C+R+R3 со сменами реакций L+R3→C на L→C+R3 (в) и с R3→C+R на C+R3→R, а затем на C→R+R3 (г). К известной ранее эвтектико-перитектической трансформации области L+C+R3 добавлены аналогичные сведения по двум областях с расплавом и трем – без расплава. R - твердый раствор R1=TiIr и R2=TiRu=R.

5. Выполнена проверка справочника по диаграммам состояния для бессвинцовых припоев [Atlas of Phase Diagrams for Lead-Free Soldering compiled by Dinsdale A. et al. COST 531, ESF. Brno, Czech Republic, 2008. V. 1].

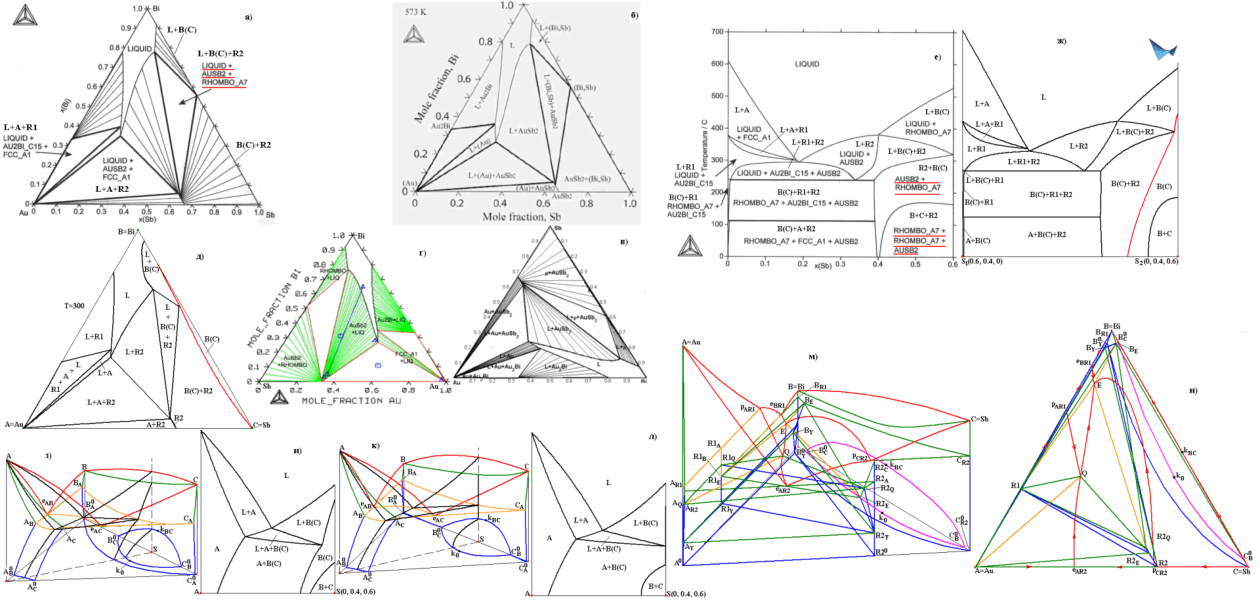
Рис. 6. В отличие от [Wang J. et al, J. Electron Mater. 2007. V. 36. No 5. P. 568] (б) и [http://td.chem.msu.ru/?page_id=638] (г), на разрезе 300^оС ФД Au-Bi-Sb в [Atlas…]) (а) и в [Manasijevića D. et al, J. of Physics and Chemistry of Solids. 2008. V. 69. No 4. P. 847] (в), а также на политермическом разрезе z_2(Bi)=0.4 [Atlas..] (е) пропущены поверхности солидуса s_В(С) и сольвуса v_В(C)R2. На разрезах (д,ж) компьютерной модели (м,н) пропущенные поверхности выделены красным). При поиске ошибок использован прототип ФД с «правильной» B_AC_AC⁰_AB⁰_A (з,и) и «неправильной» B_AC_AC⁰_AC⁰_Bk₀B⁰_CB⁰_A (к,л) поверхностью сольвуса.

6. При дизайне керамик производится анализ концентрационных полей, получаемых при проецировании фазовых областей на основание ФД. Сопоставлением последовательности фазовых превращений и наборов микроструктурных элементов в закристаллизовавшемся в равновесных условиях расплаве выявляются поля с совпадающими наборами схем кристаллизации и микроструктурами и поля с различием в этих характеристиках.

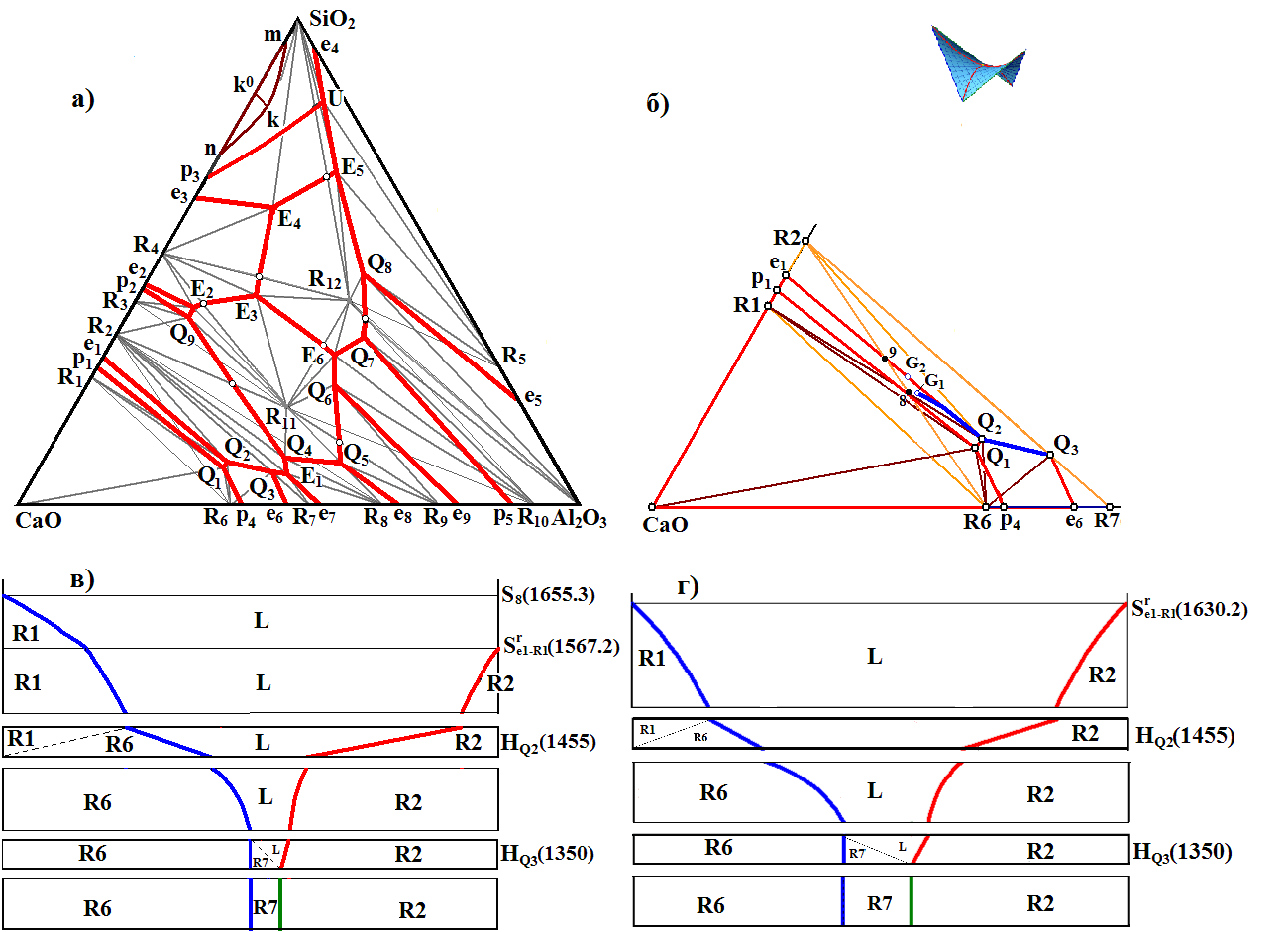
Рис. 7. XY-проекция ФД CaO-SiO₂-Al₂O₃ (а) и ее фрагмент со схемой кристаллизации состава G₁∈Q₂-8-9 (б), матбалансы для составов G₁∈Q₂-8-9 (в) и G₂∈Q₂-9 (г) (поле Q₂-9 совпадает по микроструктуре с Q₂-8-9, но отличается отсутствием реакции L¹→R₁¹, т.к. принадлежит линии ликвидуса e₁Q₂; R₁=C₃S, R₂=C₂S, R₃=C₃S₂, R₄=CS, R₅=A₃S₂, R₆=C₃A, R₇=C₁₂A₇, R₈=CA, R₉=CA₂, R₁₀=CA₆, R₁₁=C₂AS, R₁₂=CAS₂). В системе CaO-SiO₂-Al₂O₃ выявлено 117 двухмерных, 163 одномерных и 45 нульмерных полей. Поля ликвидусов CaO, C₃S, C₃A, SiO₂^сr (кристобалит), SiO₂^tr (тридимит), A₃S₂ и купола расслаивания делятся в проекции на 104 концентрационных поля: двух- (34), одно- (49) и нуль- (21) мерные), среди которых 31 поле (2 двух-, 20 одно- и 9 нульмерных) не имеют уникальных наборов микроструктуры.

7. Производится совершенствование пространственных моделей для извлечения скрытых в ФД сведений.

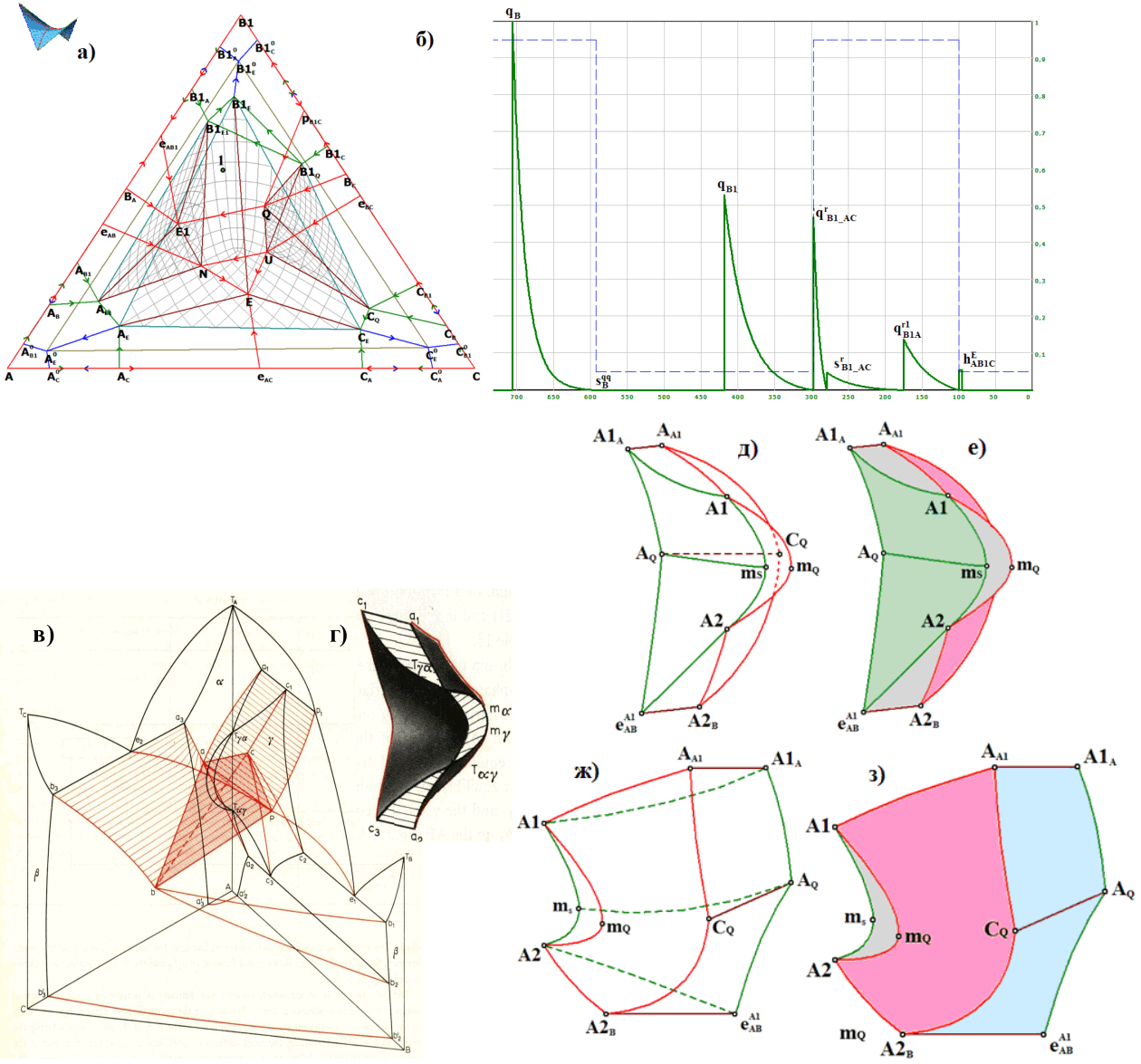
Рис. 8. Имитация спектров ДТА и электропроводности (а-б) для состава 1 в системе с полиморфным превращением компонента В. Техническое задание (д-з) для прототипирования фазовой области α+γ и лазерной визуализации конод. Пластилиновая модель (г) такой области (в) по А.Принсу [A.Prince. Alloy Phase Equilibria. 1966].

Важнейшие публикации:

1. Lutsyk V.I., Vorob’eva V.P. Relation between the Mass-Centric Coordinates in the Multicomponent Salt Systems //Z. Naturforsch. A. 2008. Vol. 63a. No 7-8. P. 513-518.

2. Луцык В.И., Зырянов А.М., Зеленая А.Э. Построение компьютерной модели Т-х-у диаграммы с моновариантным монотектическим равновесием //Журн. неорган. химии. 2008. Т. 53. № 5. С. 858-863.

3. Lutsyk I.V., Zelenaya A.E., Zyryanov A.M. Multicomponent systems simulation by the software of “Diagrams Designer” //Journal Materials, Methods & Technologies. International Scientific Publications. 2008. Vol. 2. Part 1. P. 176-184.

4. Lutsyk V.I., Vorob’eva V.P., Zelenaya A.E. T-x-y computer models with SiC and SiO2 //Electrochem. Soc. Transactions. 2009. V. 19. No 2. P. 511-524.

5. Луцык В.И., Зеленая А.Э., Зырянов А.М. Компьютерное моделирование тройных изобарных систем с расслоением расплава Au-Rh //Перспективные материалы. 2009. № 7. С. 194-198.

6. Луцык В.И., Воробьева В.П. Конструирование структуры гетерогенного материала с инвариантным превращением и сменой знака приращения одной из масс трехфазной области //Перспективные материалы. 2009. № 7. С. 199-203.

7. Lutsyk V.I., Vorob’eva V.P., Nasrulin E.R. T-x-y Diagrams with Primary Crystallization Fields of Low-Temperature Modifications //Crystallography Reports. 2009. V. 54. No 7. P. 1289-1299.

8. Lutsyk V.I., Zelenaya A.E., Zyryanov A.M. Specific Features of the Crystallization of Melts in Systems with a Transition from Syntectic Equilibrium to Monotectic Equilibrium //Crystallography Reports. 2009. V. 54. No 7. Р. 1300–1307.

9. Lutsyk V.I., Vorob’eva V.P. Computer models of eutectic type T-x-y diagrams with allotropy. Two inner liquidus fields of two low-temperature modifications of the same component //Journal of Thermal Analysis and Calorimetry. 2010. V. 101. No 1. P. 25-31.

10. Луцык В.И., Воробьева В.П. Смена знака приращения массы при перемещении трех горизонтальных материальных точек по прямолинейным направляющим //Вестник Вост.-Сиб. гос. технол. ун-та. Улан-Удэ, 2010. № 1. С. 21-25.

11. Луцык В.И., Воробьева В.П. Компьютерные модели T-x-y диаграмм эвтектического типа с полиморфным превращением одного из компонентов //Вестник Казанск. гос. технол. ун-та. Казань, 2010. № 2. С. 7-10.

12. Луцык В.И., Воробьева В.П. Исследование условий смены типа трехфазного превращения в системе Ti-Ir-Ru //Перспективные материалы. 2011. № 13. С. 191-197.

13. Луцык В.И., Зеленая А.Э. Насрулин Э.Р. Фазовые равновесия на огранении системы Pb-Sn-Cd-Bi //Перспективные материалы. 2011. № 13. С. 506-513.

14. Луцык В.И. Кристаллизационный путь как генотип многокомпонентного материала //Вестник БНЦ СО РАН. 2012. № 1(5). С. 78-97.

15. Луцык В.И., Воробьева В.П. Топологические и геометрические тренды в конструировании фазовых равновесий //Вестник БНЦ СО РАН. 2012. № 4(8). С. 212-229.

16. Lutsyk V.I., Zelenaya A.E., Savinov V.V. Melt Solidification in the Ceramic System СаО-Аl2О3-SiО2 //IOP Conf. Ser.: Mater. Sci. Eng. 2011. Vol. 18. No 11 (http://iopscience.iop.org/1757-899X/18/11/112005/pdf/1757-899X_18_11_112005.pdf).

17. Lutsyk V.I., Vorob'eva V.P. T-x-y Diagrams Computer Models for Lead-Free Soldering Systems //IOP Conf. Ser.: Mater. Sci. Eng. 2011. Vol. 18. No 9 (http://iopscience.iop.org /1757-899X/18/9/092016/pdf/1757-899X_18_9_092016.pdf ).

18. Lutsyk V.I., Vorob'eva V.P. Matrix Solution for Polyhedration of Na-K-Ca-Cl-N-O, Na-K-Mo-W-F-O and Na-Ba-B-F-O Systems //IOP Conf. Ser.: Mater. Sci. Eng. 2011. Vol. 18. No 22 (http://iopscience.iop.org/1757-899X/18/22/222005/pdf/1757-99X_18_ 22_222005.pdf).

19. Lutsyk V.I., Sumkina O.G., Savinov V.V., Zelenaya A.E. Precision of the Eutectic Points Determination by the Isopleths //IOP Conf. Ser.: Mater. Sci. Eng. 2011. Vol. 18. No 16 (http://iopscience.iop.org/1757-899X/18/16/162021/pdf/1757-899X_18_16_ 162021.pdf).

20. Луцык В.И., Зеленая А.Э., Воробьева В.П. Модернизация методов поиска легкоплавких составов в многокомпонентных солевых системах //Вопросы химии и химической технологии. (Науч.-техн. журн. НАН Украины). 2011. № 4. С. 34-36.

21. Lutsyk V.I., Zelenaya A.E., Savinov V.V. Phase Trajectories in CaO-Al2O3-SiO2 melts //Crystallography Reports. 2012. Vol. 57. No 7. P. 71-74.

22. Lutsyk V.I., Zelenaya A.E., Zyryanov A.M. Search of Low-Temperature Solvents Using Nonplanar Tie-Lines //Crystallography Reports. 2012. Vol. 57. No 7. P. 111-114.

23. Lutsyk V.I., Vorob’eva V.P., Sumkina O.G. Triangulation of Salt Systems with Barium Borate //Crystallography Reports. 2012. Vol. 57. No 7. P. 115-125.

24. Lutsyk V.I., Nasrulin E.R. Competition of Primary and Eutectic Crystals in Invariant and Univariant Reactions //Crystallography Reports. 2012. Vol. 57. No 7. P. 106-110.

25. Lutsyk V., Zelenaya A. Improvement of the Method to Search Low-melting Solvents for the Crystals MВаNa(ВО3)2 (M=Sc,Y) Growth //Solid State Science. 2012. Issues 11-12. P. 1604-1608.

26. Lutsyk V.I., Vorob’eva V.P. Reasons for Contradiction of T-x-y Diagram Au-Bi-Sb //Scientific Journal (ISSN 2304-1862) “Proceedings of the International Conference NANO Materials: Applications & Properties”. 2012. Vol. 1. No 4. P. 04NMEEE02-1 – 04NMEEE02-4.

27. Lutsyk V., Zelenaya A. Crystallization Paths and Microstructures in Ternary Oxide Systems with Stoichiometric Compounds //Solid State Phenomena. 2013. Vol. 200. P. 73-78.

28. Lutsyk V., Vorobjeva V., Parfenova M.. Quaternary Reciprocal Systems with the Inner Diagonals: Variants of Polyhedration //Advanced Materials Research. 2013. Vol. 704. P. 55-60.

29. Lutsyk V., Zelenaya A., Parfenova M. Solidification Paths in the Ceramic Systems //Advanced Materials Research. 2013. Vol. 704. P. 173-178.

30. Lutsyk V., Zelenaya A., YaZhou Dai. Li,Na,K,La||F System for Molten Salt Reactor: 3D and 4D Computer Models //Advanced Materials Research. 2013. Vol. 704. P. 349-352.

31. Lutsyk V.I., Vorob’eva V.P. 3D computer models of Mo-Zr-V, Ti-C-V, Ti-Ir-Ru T-x-y diagrams with three-phase reaction type changing //Scientific Journal (ISSN 2304-1862) “Proceedings of the International Conference NANO Materials: Applications & Properties”. 2013. Vol. 2. No 4. P. 04NAESP07-1–04NAESP07-4.

32. Lutsyk V.I., Zelenaya A.E. Ternary Systems for the Liquid Immiscibility Gap Technology //Scientific Journal (ISSN 2304-1862) “Proceedings of the International Conference NANO Materials: Applications & Properties”. 2013. Vol. 2. No 4. P. 04NAESP09-1–04NAESP09-4.

Патенты, изобретения:

1. Насрулин Э.Р., Луцык В.И., Воробьева В.П. Компьютерная программа "Автоматизация анализа фазовой диаграммы с бинарным инконгруэнтным соединением" // Свидетельство Отраслевого фонда алгоритмов и программ № 3902. Инновации в науке и образовании. – 2006, №7, реф. 3902. http://ofap.ru/portal//innovat/n7_2005/n7_2005.html

2. Насрулин Э.Р., Луцык В.И., Воробьева В.П. Компьютерная программа "Визуализация путей кристаллизации и расчет материального баланса в тройных фазовых диаграммах" // Свидетельство Отраслевого фонда алгоритмов и программ № 6632. Инновации в науке и образовании. – 2006, №7, реф. 6632. http://ofap.ru/portal//innovat/n7_2005/n7_2005.html

3. Насрулин Э.Р., Луцык В.И. Компьютерная программа "Редактор тройных фазовых диаграмм, состоящих из произвольного числа поверхностей с выпуклым прямолинейным контуром" // Свидетельство Отраслевого фонда алгоритмов и программ № 6596. Инновации в науке и образовании. – 2006, №7, реф. 6596. http://ofap.ru/portal//innovat/n7_2005/n7_2005.html

Официальное признание:

1. Для Второй Международной конференции по конкурентным материалам и технологическим процессам (2nd International Conference on Competitive Materials and Technology Processes IC-CMTP2, Miskolc (Hungary), Oct 8-12, 2012) подготовлена научная сессия «Фазовая диаграмма как инструмент материаловедения» (Session 11 “Phase Diagram as a Tool of Materials Science”. Session Chair Vasily Lutsyk), http://ic-cmtp2.eu/subjects.php?contr=&kod=&ide=11&title= Phase%20Diagram%20as%20a%20Tool%20of%20Materials%20Science. Аналогичная сессия готовится для 3nd International Conference on Competitive Materials and Technology Processes IC-CMTP3 (Miskolc, Hungary, Oct 6-10 2014) http://www.ic-cmtp3.eu/subjects.php?contr=&kod=&ide=52&title=Session%2013:%20%20Phase%20Diagram%20as%20a%20Tool%20of%20Materials%20Science.

2. Заключено соглашение о техническом сотрудничестве ИФМ СО РАН с фирмой КНР “Maanshan Ridery Ceramic New Material Technology Co., Ltd.” (www.rdrd188.cn, www.rdrd168.com).

3. Получено свидетельство № 04-01280 ФГБНУ НИИ РИНКЦЭ Министерства образования и науки Российской Федерации о регистрации в федеральном реестре экспертов научно-технической сферы Луцыка В.И.

4. В.И.Луцык, А.Э.Зеленая, А.М.Зырянов включены в список спикеров, http://www.enfuture.ru/enfuture/c15 http://www.enfuture.ru/enfuture/c21, Международных молодежных машиностроительных форумов "Инженеры будущего", организуемых Союзом машиностроителей России, для проведения образовательного сервиса «Дизайн керамик и сплавов». Партнер Форумов "Инженеры будущего" – Институт физического материаловедения СО РАН, http://www.enfuture.ru/services/23.

Связь с вузами:

1. Для Министерства образования и науки Республики Бурятия выполнен проект "Мониторинг обучения при помощи электронных версий традиционных учебников" (2007, рук. Зеленая А.Э.).

2. Разработаны спецкурсы и изданы учебные пособия для выполнения интеграционных (междисциплинарных) проектов в области физико-химического материаловедения студентами Бурятского госуниверситета (химический факультет, институт математики и информатики).

3. Дипломант Института математики и информатики БГУ Н.Г.Червякова (научный руководитель В.И.Луцык) выступила с докладом на Международной конференции «Second European Conference and Exhibition on Advanced Materials and Technologies» (2001, Bucharest, Romania).

4. Бакалавр Института математики и информатики БГУ В.И.Степанов (научный руководитель В.И.Луцык) выступил с докладом на Международной конференции «Junior Euromat 2008» (14-18 July, 2008; Lausanne, Switzerland).

5. Заключено Соглашение о стратегическом партнерстве ИФМ СО РАН c федеральным государственным бюджетным образовательным учреждением высшего профессионального образования “Санкт-Петербургский государственный политехнический университет” (СПбГПУ, http://www.kafedra-cm.ru/0,0/kafedra-tcm).

6. Разработаны инновационные образовательные технологии «обучающий ЕГЭ» и «образовательный пандус» (http://ctj.isuct.ru/files/2012/v55_n09_2012_abstracts_en.pdf, http://ctj.isuct.ru/?q=node/2047).

7. Разработаны методические, учебные и учебно-методические пособия:

Луцык В.И. Химическая термодинамика в формулах. Мет. пособие. Улан-Удэ: изд-во БГУ. 2000. 22 с.
Луцык В.И. Конструирование многокомпонентных систем. I. T-x-y диаграммы с 25-ю поверхностями. Уч.-мет. пособие. Улан-Удэ: изд-во БГУ. 2000. 25 с.
Луцык В.И. Конструирование многокомпонентных систем. II. T-x-y-z диаграммы с 71-й гиперповерхностью. Уч.-мет. пособие. Улан-Удэ: изд-во БГУ. 2000. 27 с.
Луцык В.И., Зеленая А.Э., Григорьев И.Г. Объектно-ориентированное конструирование многокомпонентных систем. Уч. пособие. Улан-Удэ: изд-во БГУ, 2001. 40 с.
Луцык В.И., Воробьева В.П., Сумкина О.Г. Дизайн материалов с инконгруэнтными фазами. Уч. пособие. Улан-Удэ: изд-во БГУ, 2002. 102 с.
Луцык В.И., Урмакшинова Е.Р., Мохосоев Б.В. Автоматизация графики Д.А.Петрова для T-x-y-z диаграмм эвтектического типа. Уч.-метод. пособие. Улан-Удэ: изд-во БГУ, 2003. 46 с.
Луцык В.И. Термодинамические задачи. Уч. пособие. Улан-Удэ: изд-во БГУ. 2003. 84 с.
Луцык В.И., Зырянов А.М. Барицентрические задачи. Уч. пособие. Улан-Удэ: изд-во БГУ, 2004, 105 с.
Луцык В.И., Воробьева В.П. Визуализация физико-химических систем. Уч.-мет. пособие. Улан-Удэ: изд-во БГУ, 2007. 100 с.
Воробьева В.П. Численные методы в химии. Уч. пособие. Улан-Удэ: изд-во БГУ, 2007. 85 с.
Воробьева В.П. Практикум по курсу «Численные методы и языки программирования». Уч.-мет. пособие. Улан-Удэ: изд-во БГУ, 2007. 87 с.
Луцык В.И., Зырянов А.М., Зелёная А.Э. Конструирование Т-х-у диаграмм кинематическими поверхностями. Уч. пособие. Улан-Удэ: изд-во БГУ, 2007. 80 с.